OPTIQUE - Optique non linéaire

OPTIQUE - Optique non linéaire

L’optique non linéaire est l’ensemble des phénomènes qui résultent de la non-linéarité de la réponse d’un milieu matériel à l’action d’une onde électromagnétique du domaine optique. Elle est une conséquence de l’invention du laser: le premier exemplaire a été construit en 1960; la première expérience d’optique non linéaire fut faite en 1961 (génération de second harmonique); dès 1962, la plupart des effets de l’optique non linéaire étaient expliqués théoriquement.

Le champ électrique d’une onde électromagnétique polarise tout système matériel. En champ fort, ce qui explique la nécessité de l’emploi du laser, la polarisation induite dévie du régime linéaire valable en champ faible. Certains effets de l’optique non linéaire sont la transposition en optique d’effets déjà connus à plus basse fréquence: génération d’harmoniques, amplification paramétrique. D’autres sont l’équivalent d’effets déjà connus en résonance magnétique nucléaire. Mais certains sont propres à l’optique, comme l’effet Raman stimulé, découvert par hasard. Ce qui est caractéristique de l’optique non linéaire, c’est l’importance du phénomène de propagation.

1. Susceptibilités non linéaires

Les ondes rencontrées en optique non linéaire sont, en général, assez intenses pour que les champs électromagnétiques puissent être traités classiquement. La quantification du champ n’est nécessaire que pour traiter les processus spontanés (par exemple: luminescence paramétrique, diffusion Raman, etc.) qui initient certains phénomènes de l’optique non linéaire. En revanche, la matière est en général traitée quantiquement. Dans un milieu matériel non chargé et non conducteur, les équations de Maxwell macroscopiques s’écrivent:

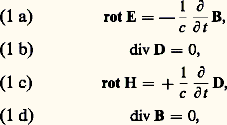où E et H sont les champs électriques et magnétiques et où D et B sont les inductions correspondantes. D et B s’expriment sous forme de développements multipolaires:

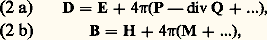où P, Q, M sont respectivement les densités de moment dipolaire électrique, de moment quadrupolaire électrique et de moment dipolaire magnétique. Bien que les termes quadrupolaire électrique et dipolaire magnétique donnent parfois naissance à des effets intéressants, l’essentiel des phénomènes d’optique non linéaire est dû au terme dipolaire électrique. On négligera donc tous les moments autres que P.

En optique conventionnelle, le champ électrique est suffisamment faible pour que l’on puisse écrire, avec une très bonne approximation, que la densité de polarisation induite est proportionnelle au champ électrique. Lorsque le champ E est plus fort, P peut être décomposé en puissances de E:

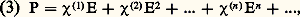où 﨑^{(n )} est la susceptibilité d’ordre n dont on néglige momentanément le caractère tensoriel. Dans le développement (3), le rapport entre un terme et le terme précédent est de l’ordre de E/E^at, où E^at est le module du champ intra-atomique. Dans un faisceau laser d’une intensité de 100 MW/cm², E est de l’ordre de 10³u.é.s. alors que E^at est de l’ordre de 10⁷ à 10⁸u.é.s.

La réponse de la matière n’étant pas instantanée, il est nécessaire de décomposer E et P en leurs composantes de Fourier. Par exemple, la composante P size=1^猪(2) ( 諸) de la polarisation au deuxième ordre, à la fréquence 諸, s’écrit:

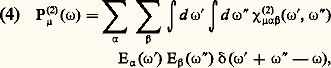la somme sur 見 et 廓 étant étendue aux trois composantes x , y et z ; 嗀 est la fonction de Dirac. Le calcul des susceptibilités se fait par la méthode des perturbations. Si le milieu est constitué de systèmes microscopiques (par exemple des atomes), on calcule d’abord les polarisabilités d’un système microscopique. Loin de toute résonance, on obtient ce résultat, dans l’approximation dipolaire électrique:

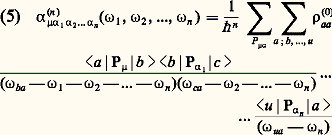où P size=1^猪見 désigne toute permutation des couples ( 猪, 諸 size=1^靖), ( 見¹, 諸¹), ..., ( 見ⁿ , 諸ⁿ ); 諸 size=1^靖 = 漣 諸¹ 漣 諸² 漣 ... 漣 諸ⁿ ; a , b , ..., u sont tous les états du système; 福⁽⁰⁾aa la population du niveau a et P l’opérateur moment dipolaire électrique. Dans ce cas, 見^{(n )} est réel et invariant par toute permutation du groupe 戮 size=1^猪見.

Connaissant la polarisabilité d’ordre n , 見^{(n )}, d’un système microscopique, la susceptibilité d’ordre n , 﨑^{(n )}, s’obtient en multipliant 見^{(n )} par le nombre N de systèmes par unité de volume et en appliquant la correction de champ local. La correction de champ local est souvent complexe, mais 﨑^{(n )} possède la même propriété de symétrie que 見^{(n )}. Au voisinage d’une ou de plusieurs résonances, l’expression (5) de 見^{(n )} n’est plus valable, car il faut tenir compte de l’amortissement: 見^{(n )} est alors complexe et n’est plus invariant par les permutations du groupe 戮 猪見.

﨑^{(n )} est un tenseur caractéristique du milieu matériel. Ce tenseur est donc invariant par toute opération faisant partie du groupe de symétrie du milieu, ce qui entraîne que, parmi les 3^{n +1} composantes de 﨑^{(n )}, très peu sont indépendantes et beaucoup sont nulles en général. Ainsi, si le milieu possède un centre d’inversion, 﨑⁽²⁾ et tous les 﨑^{(n )} d’ordre pair sont identiquement nuls. 﨑⁽²⁾ est donc nul dans les fluides et dans les verres; il n’est non nul que pour vingt et une des trente-deux classes de cristaux.

2. Propagation dans un milieu non linéaire

L’équation de propagation d’une onde de fréquence 諸 dans un milieu non linéaire s’obtient à partir des équations de Maxwell (1 a) et (1 c). Elle s’écrit:

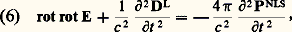où le terme linéaire P⁽¹⁾ a été séparé des termes non linéaires et inclus dans D^L. Le terme P^NLS (NLS pour non linear source ) qui joue le rôle de terme source dans le membre de droite de (6) est en général créé par des ondes planes de fréquence 諸¹, 諸², ..., 諸ⁿ et de vecteur d’onde k¹, k², ..., kⁿ , avec 諸 = 諸¹ + 諸² + ... + 諸ⁿ ; le terme P^NLS est alors de la forme:

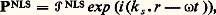où k^s = k¹ + k² + ... + kⁿ . La solution de (6) est la somme d’une solution particulière de l’équation totale (solution forcée en exp (i k^s 練 r)) et de solutions de l’équation sans second membre (ondes libres en exp (i k^L 練 r)). En général, on peut considérer que le milieu non linéaire emplit le demi-espace de droite de la figure 1, le demi-espace de gauche étant empli par un milieu linéaire (souvent le vide). La solution de (6) doit satisfaire les conditions de continuité des composantes tangentielles de E et de H sur le plan de séparation d’équation z = 0, ce qui implique l’existence d’une onde réfléchie dans le milieu linéaire (onde libre en exp (i k^R 練 r)): c’est le phénomène de la réflexion non linéaire. Pour que les conditions de continuité soient satisfaites, il faut que k^L et k^R aient la même composante tangentielle que k^S. Par conséquent, k^L 漣 k^S est normal au plan de séparation. D’autre part, k^S est imposé par les ondes incidentes, le module de k^L est imposé par la relation de dispersion du milieu de droite et le module de k^R par la relation de dispersion du milieu de gauche. Cela conduit au calcul de ^L et ^R, c’est-à-dire à des relations de Descartes généralisées.

L’onde réfléchie est très peu intense, parce que seule une épaisseur de l’ordre de la longueur d’onde lui donne naissance. Mais elle est très importante dans le cas de milieux non transparents, car elle seule permet l’étude des susceptibilités non linéaires de ces milieux. Inversement, dans le cas de milieux transparents, elle est négligeable.

Il est important de remarquer que le sens du transfert d’énergie dépend de la phase relative de P^NLS et de E. Suivant les cas, l’onde de fréquence 諸 est amplifiée ou atténuée. Pour que le transfert d’énergie ait un sens constant, il faut que la phase relative de P^NLS et de E soit constante: c’est le problème très important de l’adaptation de phase qui se traduit par k^L = k^S.

L’équation (6) peut aussi se résoudre avec une bonne approximation en écrivant le champ électrique sous la forme:

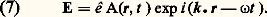Si P^NLS = 0, il s’agit alors d’une onde libre d’amplitude constante, de vecteur d’onde k et de polarisation ê . Le terme source P^NLS fait que l’amplitude ou enveloppe A(r, t ) est fonction de la position et du temps. Mais, en règle générale, A varie lentement dans l’espace et dans le temps, ce qui permet de négliger les dérivées secondes et d’obtenir l’équation approchée (fig. 2):

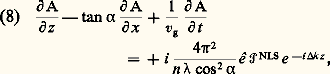où 見 est l’angle de biréfringence (angle entre le vecteur d’onde k et le vecteur de Poynting), v^g la vitesse de groupe à la fréquence 諸, n l’indice à la fréquence 諸, = 2 神c / 諸 et k = k 漣 k^S en supposant, pour simplifier, que k^S est parallèle à Oz . L’interprétation du membre de gauche de l’équation (8) est simple. Le terme en tan 見(face=F0019 煉A/ 煉x ) indique que la direction de propagation de l’énergie fait un angle 見 avec le vecteur d’onde et le terme en (1/v^g ) (face=F0019 煉A/ 煉t ) indique qu’une impulsion lumineuse se propage à la vitesse de groupe. S’il est parfois nécessaire d’avoir recours à l’équation exacte (6) pour résoudre le problème de la propagation dans un milieu non linéaire, souvent l’équation approchée (8) est une approximation suffisante.

3. Phénomènes du deuxième ordre

Création de deuxième harmonique

Lorsqu’un faisceau laser de fréquence 諸¹ est incident sur un matériau non linéaire possédant un 﨑⁽²⁾ non nul, il donne naissance à une polarisation non linéaire de fréquence 諸² = 2 諸¹. Cette polarisation rayonne une onde de fréquence 2 諸¹: c’est la génération de second harmonique. Si on suppose que l’onde laser est une onde plane monochromatique, on peut résoudre l’équation (6) en faisant 諸 = 諸² et obtenir ainsi l’amplitude de l’onde réfléchie et celle de l’onde transmise. L’étude de l’harmonique en réflexion est importante dans le cas de milieux opaques (semiconducteurs) car elle seule permet la mesure de 﨑⁽²⁾. Mais, pour un milieu transparent, l’amplitude de l’onde réfléchie est négligeable et l’équation (8) associée à la condition aux limites A² nul pour z = 0 donne avec une bonne précision l’évolution de l’onde harmonique.

En écrivant E¹, sous la forme:

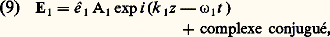l’expression de P^NLS est la suivante:

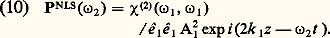L’intensité à la distance z de la face d’entrée de l’onde harmonique créée est proportionnelle à

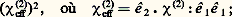elle est aussi proportionnelle au carré de l’intensité de l’onde fondamentale et enfin à (sin²( k z /2))/( k /2)², où k = k ² 漣 2 k ¹; k ² est le module du vecteur d’onde d’une onde libre de fréquence 諸² (k ² = n ( 諸²) 諸²/c , alors que k ¹ = n ( 諸¹) 諸¹/c ). Si k 0, il n’y a pas adaptation de phase. L’intensité harmonique croît d’abord à partir de zéro, atteint un premier maximum en z = l ^c = 神/ k , puis décroît, s’annule à nouveau en z = 2 l ^c, puis croît encore, etc.; l ^c est appelé longueur de cohérence. Si on tourne le cristal, la distance parcourue par l’onde fondamentale varie et l’intensité harmonique oscille: c’est ce que l’on appelle les franges de Maker. Par contre, si k = 0, l’intensité de l’onde harmonique est proportionnelle à z ², c’està-dire qu’elle croît constamment (fig. 3).

Dans le cas de la génération d’harmonique, la condition k = 0 est équivalente à n ( 諸²) = n ( 諸¹). Dans un milieu isotrope, n ( 諸²) est supérieur à n ( 諸¹) à cause de la dispersion normale et il n’est pas possible d’obtenir l’adaptation de phase. On peut obtenir l’adaptation de phase pour certains cristaux anisotropes. Par exemple, pour un cristal uniaxe négatif, en choisissant le mode ordinaire pour l’onde fondamentale et le mode extraordinaire pour l’onde harmonique. L’indice n ( 諸²) dépend alors de l’angle entre l’axe optique et le vecteur d’onde de l’onde harmonique: il décroît régulièrement de n ^o( 諸²), indice ordinaire pour = 0, à n ^e ( 諸²), indice extraordinaire pour = 神/2. Si n ^o( 諸¹) est compris entre n ^o( 諸²) et n ^e ( 諸²), il existe un angle ^m pour lequel les indices pour les deux ondes sont égaux.

Si l’onde fondamentale n’est pas de durée infinie mais si l’on a affaire à une impulsion, cette impulsion fondamentale donne naissance à une impulsion harmonique. Même s’il y a adaptation de phase, c’est-à-dire égalité des vitesses de phase à 諸¹ et 諸² = 2 諸¹, les vitesses de groupe ne sont pas égales à 諸¹ et 諸². La vitesse de phase v 﨏 est égale à 諸/k et la vitesse de groupe v^g à d 諸/dk . Si, par exemple, v^g 2 est inférieur à v^g 1, l’impulsion harmonique créée dans les premières tranches du cristal se propage moins vite que l’impulsion fondamentale. À partir d’une certaine distance, ces deux impulsions ne coïncident plus dans le temps et l’impulsion harmonique n’est plus amplifiée. L’impulsion fondamentale donne naissance dans les différentes tranches du cristal à une série d’impulsions harmoniques. À la sortie du cristal, on obtient une impulsion harmonique plus longue que l’impulsion fondamentale: c’est l’effet de groupe. Pratiquement, pour un cristal de quelques centimètres d’épaisseur, l’effet de groupe ne se traduit que pour des impulsions ultracourtes, d’une durée de l’ordre de la picoseconde (10^-12 s). Théoriquement, l’effet de groupe se décrit simplement grâce au terme (1/v^g )(face=F0019 煉A/ 煉t ) de l’équation (8). Connaissant la forme de l’impulsion fondamentale, on en déduit celle de l’impulsion harmonique.

Si l’onde fondamentale n’est pas une onde plane mais possède une extension finie dans la direction x (fig. 2) et s’il y a adaptation de phase avec, par exemple, l’onde fondamentale ordinaire et l’onde harmonique extraordinaire, le pinceau lumineux fondamental ne se propage pas dans la même direction que le pinceau lumineux harmonique. Le pinceau harmonique créé dans les premières tranches du cristal quitte progressivement le pinceau fondamental et n’est plus amplifié. Le pinceau fondamental donne naissance dans les différentes tranches du cristal à une série de pinceaux harmoniques et on obtient, à la sortie du cristal, un faisceau harmonique d’extension spatiale (suivant x ) plus grande que celle du faisceau fondamental: c’est l’effet de biréfringence.

L’effet de biréfringence s’analyse simplement grâce au terme tan 見(face=F0019 煉A/ 煉x ) de l’équation (8). Le traitement mathématique de cet effet est identique à celui de l’effet de groupe. Il est parfois possible, pour certains cristaux et certaines fréquences, d’avoir adaptation de phase avec = 神/2. Dans ce cas, l’angle de biréfringence 見 est nul et il n’y a pas d’effet de biréfringence. On dit qu’il y a adaptation de phase non critique. Pour réaliser la condition n ( 諸²) = n ( 諸¹), on joue sur la température du cristal.

L’énergie de l’onde harmonique est prise à l’onde fondamentale. L’approximation qui consiste à supposer A¹ constant n’est valable que tant que l’intensité de l’harmonique est négligeable devant celle du fondamental. C’est, en général, le cas quand il n’y a pas adaptation de phase. Mais, s’il y a adaptation de phase, la croissance en z ² de l’intensité de l’onde harmonique n’est pas réaliste: elle ne peut avoir lieu qu’au début du cristal. Il faut tenir compte de la réaction de l’onde harmonique sur l’onde fondamentale. Le champ électrique de l’onde fondamentale étant sous la forme (9) et celui de l’onde harmonique:

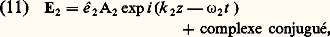(A¹ et A² dépendent de z ), il se crée, dans le milieu, une polarisation du deuxième ordre à la fréquence 諸¹ qui s’écrit:

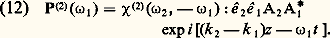S’il y a adaptation de phase, k ² = 2 k ¹, et les deux équations couplées qui régissent l’évolution de A¹ et de A² se résolvent exactement. En supposant A¹(0) réel:

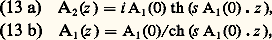où s = (4 神²/n²) 﨑^eff, n étant la valeur commune à n ( 諸¹) et n ( 諸²). L’intensité harmonique est donc en th² ( z ) et la fondamentale en 1/ch² ( z ): l’intensité totale ne dépend pas de z ; l = 1/ = 1/s A¹(0) s’appelle longueur caractéristique d’interaction et est de l’ordre du centimètre pour une intensité fondamentale incidente de l’ordre de 100 MW/cm². Les équations (13 a) et (13 b) montrent que le transfert d’énergie de l’onde fondamentale vers l’onde harmonique est théoriquement total (fig. 4).

L’onde fondamentale de fréquence 諸¹ donne aussi naissance à une polarisation d’ordre 2 de fréquence 0, c’est-à-dire statique: c’est le redressement optique qui a été observé expérimentalement mais qui est de peu d’intérêt pratique.

Mélange de fréquences

Si deux ondes de fréquence 諸¹ et 諸² sont incidentes sur le cristal, elles donnent naissance à des polarisations d’ordre 2 de fréquences 諸¹ + 諸² et 諸¹ 漣 諸²: on parle de génération de fréquence somme dans le premier cas et de fréquence différence ou battement dans le second. Ces deux phénomènes présentent les mêmes propriétés que la génération de deuxième harmonique. En particulier, pour qu’il y ait transfert important d’énergie vers la fréquence somme ou vers la fréquence différence, il faut qu’il y ait adaptation de phase.

Amplificateur et oscillateur paramétriques

En ce qui concerne les amplificateurs et les oscillateurs paramétriques, on a affaire à l’interaction de trois ondes de fréquence 諸¹, 諸² et 諸³ = 諸¹ + 諸². Dans certaines conditions (par exemple si A² est nul en z = 0), l’onde de fréquence 諸³, appelée onde pompe, peut amplifier l’onde de fréquence 諸¹, appelée onde signal, et l’onde de fréquence 諸², appelée onde complémentaire. On est alors en présence de trois équations couplées qui impliquent que S¹, S² et S³, intensités des ondes signal, complémentaire et pompe, vérifient les relations de Manley-Rowe:

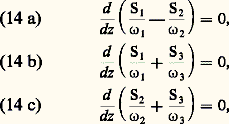relations qui s’interprètent en termes de photons: chaque fois qu’un photon pompe est détruit, un photon signal et un photon complémentaire sont créés.

Si l’onde pompe est peu atténuée, on peut supposer A³ constant et, si A² est nul en z = 0, les deux équations deviennent (dans le cas de l’adaptation de phase):

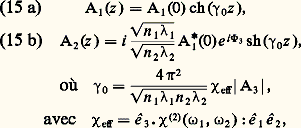et où 淋³ est l’argument de A³. Au voisinage de l’adaptation de phase, le gain est:

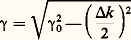où k = k ³ 漣 k ¹ 漣 k ², et l’expression de A¹(z ) et A²(z ) est légèrement plus complexe. Il y a donc amplification si 塚²⁰ 礪 ( k /2)² et le gain maximal est obtenu à l’adaptation de phase. La croissance exponentielle de l’intensité signal n’est exacte que tant que l’intensité pompe n’est pas atténuée. Il y a là aussi un phénomène de saturation.

Si on place le cristal non linéaire entre deux miroirs réfléchissant soit l’onde signal soit l’onde signal et l’onde complémentaire, on obtient un oscillateur paramétrique, simplement résonnant dans le premier cas et doublement résonnant dans le second. L’oscillateur démarre, en général, à partir des photons créés par luminescence paramétrique: c’est l’effet par lequel, dans le cristal, un photon d’énergie 寮 諸³ se désintègre spontanément en deux photons d’énergie 寮 諸¹ et 寮 諸² tels que 諸¹ + 諸² = 諸³. Le seuil d’oscillation est plus élevé pour l’oscillateur simplement résonnant que pour l’oscillateur doublement résonnant. Ce seuil peut être suffisamment faible pour que l’oscillateur fonctionne en régime continu. La fréquence 諸¹ créée par l’oscillateur est celle pour laquelle il y a adaptation de phase. En faisant varier par exemple la température du cristal, on peut faire varier 諸¹. L’oscillateur paramétrique pompé à la fréquence fixe 諸³ est une source accordable.

Pour tous ces effets du second ordre, les cristaux les plus utilisés sont le niobate de lithium (LiNbO³), le monophosphate de potassium (KH²P⁴) et des cristaux de la même famille.

4. Phénomènes du troisième ordre

Génération de troisième harmonique

Une onde laser de fréquence 諸¹ incidente sur un matériau donne naissance à une polarisation du troisième ordre de fréquence 3 諸¹ proportionnelle à 﨑⁽³⁾ ( 諸¹, 諸¹, 諸¹). Cette polarisation rayonne une onde de fréquence 3 諸¹: c’est la génération de troisième harmonique. Pour ce phénomène, on peut répéter tout ce qui a été dit à propos de la génération de second harmonique, bien que l’effet soit en général plus faible. Cet effet peut se produire dans un milieu avec centre d’inversion, par exemple un fluide. Pour accroître 﨑⁽³⁾, on cherche à s’approcher d’une résonance, ce qui diminue fortement l’un des dénominateurs de l’expression (5). Pour obtenir l’adaptation de phase, on peut parfois utiliser la dispersion anormale en mélangeant au gaz actif un gaz possédant une résonance entre 諸¹ et 3 諸¹. Une onde polarisée circulairement ne donne pas de troisième harmonique, parce qu’il n’y aurait pas conservation du moment cinétique.

Un autre effet du troisième ordre est l’amplification paramétrique à quatre ondes. Une onde pompe de fréquence 諸³ peut amplifier deux ondes de fréquences 諸¹ et 諸² telles que 2 諸³ = 諸¹ + 諸². Cet effet est dû à 﨑⁽³⁾ ( 諸³, 諸³, 漣 諸¹). Pour qu’il y ait amplification, il faut qu’il y ait adaptation de phase, c’est-à-dire 2 k³ = k¹ + k².

Indice non linéaire

Toute une classe d’effets est liée à 﨑⁽³⁾( 諸¹, 漣 諸¹, 諸²) par lequel une onde intense de fréquence 諸¹ et une onde parfois moins intense de fréquence 諸² donnent naissance à une polarisation P⁽³⁾ ( 諸²) qui vient s’ajouter au terme linéaire P⁽¹⁾ ( 諸²). L’indice à la fréquence 諸² est modifié par l’onde de fréquence 諸¹ proportionnellement à l’intensité S¹. Nous nous limitons ici au cas où 﨑⁽³⁾ ( 諸¹, 漣 諸¹, 諸²) est réel. L’indice non linéaire vient de l’anisotropie des molécules et de l’électrostriction. Dans un fluide composé de molécules anisotropes, l’onde de fréquence 諸¹ induit de la biréfringence: c’est l’effet Kerr optique.

Le cas où 諸² = 諸¹ est un cas particulier dans lequel une onde influe sur sa propre propagation. L’indice non linéaire est généralement écrit sous la forme:

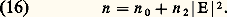Un faisceau laser n’est jamais une onde plane. Par exemple, le mode fondamental noté TEM⁰⁰ possède une répartition transverse d’intensité gaussienne. L’intensité est plus grande au centre que sur les bords. Si n ² est positif (en général), le centre du faisceau se propage moins vite: le front d’onde s’incurve et le faisceau va converger en un point; c’est le phénomène d’autofocalisation (le faisceau a créé l’équivalent d’une lentille). Plus exactement, il y a autofocalisation si le phénomène précédent l’emporte sur la diffraction. Si l’on suppose qu’il n’y a pas d’aberration, la distance focale calculée est:

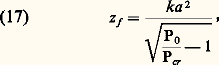où k est le module du vecteur d’onde, a le rayon du faisceau incident, P⁰ la puissance de ce faisceau et P^cr la puissance critique au-dessus de laquelle il y a autofocalisation. La puissance critique est de l’ordre de²n ⁰c /8 n ².

Le champ tend théoriquement vers l’infini quand on s’approche du foyer. En fait, il devient tellement fort qu’il y a souvent ionisation de la matière et création d’un plasma. L’autofocalisation est donc un grave problème pour les lasers de puissance.

Le champ d’une impulsion à l’entrée d’un milieu non linéaire s’écrit:

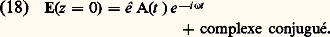Après propagation et en négligeant la déformation de l’enveloppe, ce champ devient:

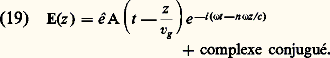Puisque n dépend de A, la phase n 諸z /c dépend du temps: c’est le phénomène d’automodulation de phase qui se produit effectivement avant la déformation de l’impulsion et qui peut conduire à un élargissement spectral considérable.

Absorption à deux photons

Si, 諸¹ et 諸² étant positifs, on a 諸¹ + 諸² 力 諸^ba , où a et b sont deux niveaux d’énergie des systèmes constituant le milieu matériel, alors 﨑⁽³⁾ ( 諸¹, 漣 諸¹, 諸²) est complexe et sa partie imaginaire est telle que, quand il n’y a pas inversion de population entre les niveaux a et b , il y a absorption à la fréquence 諸¹ et à la fréquence 諸². Le coefficient d’absorption à la fréquence 諸² est proportionnel à l’intensité S¹ (et vice versa): c’est le phénomène d’absorption à deux photons. Les photons d’énergie 寮 諸¹ et 寮 諸² sont absorbés simultanément pendant que le système passe du niveau a au niveau b .

Diffusions stimulées

Si, 諸¹ et 諸² étant positifs et 諸¹ 礪 諸², on a 諸¹ 漣 諸² 力 諸^ba , alors 﨑⁽³⁾ ( 諸¹, 漣 諸¹, 諸²) est également complexe et sa partie imaginaire est telle, toujours dans le cas normal, qu’il y a amplification à la fréquence 諸² et absorption à la fréquence 諸¹. Il s’agit encore d’une transition à deux photons; mais, ici, un photon d’énergie 寮 諸¹ est détruit pendant qu’un photon d’énergie 寮 諸² est créé et que le système passe du niveau a au niveau b : c’est l’effet Raman stimulé (le gain à la fréquence 諸² est proportionnel à l’intensité S¹). Les niveaux a et b peuvent être des niveaux de rotation ou des niveaux électroniques; mais, en général, ce sont des niveaux de vibration: on parle de diffusion Raman vibrationnelle.

L’onde 諸¹ est, en général, une onde laser et on note 諸¹ = 諸^L. L’onde de fréquence 諸^S = 諸^L 漣 諸^ba est l’onde Stokes et l’onde de fréquence 諸^A = 諸^L + 諸^ba est l’onde anti-Stokes. Il y a gain pour l’onde Stokes, mais atténuation pour l’onde anti-Stokes, qui est en général négligeable. Tous les phénomènes qui découlent d’un 﨑⁽³⁾ ( 諸¹, 漣 諸¹, 諸²) sont à adaptation de phase automatique. Le gain Raman-Stokes est isotrope, la croissance de l’onde Stokes se fait à partir des photons créés par diffusion Raman spontanée. Si le milieu matériel est placé entre deux miroirs réfléchissant à la fréquence 諸^S, on obtient un oscillateur Raman. Mais, en général, la création de l’onde Stokes se fait en un seul passage. L’onde anti-Stokes peut être créée par un processus paramétrique puisque 諸^A = 諸^L + 諸^L 漣 諸^S. Il faut qu’il y ait adaptation de phase, c’est-à-dire 2 k^L = k^S + k^A et l’onde anti-Stokes est émise en cône (fig. 5). L’effet Raman stimulé de vibration peut être traité classiquement. Ce qui précède concerne l’effet Raman en régime stationnaire. Si la durée de l’impulsion laser est plus courte que le temps de relaxation de la vibration, on est en régime transitoire. L’excitation de la vibration ayant un certain retard, l’impulsion Stokes n’a pas la même forme que l’impulsion laser: elle est plus courte, retardée et beaucoup moins énergétique que si l’on était en régime stationnaire; la notion de gain n’a plus de sens. Les diffusions spontanées Brillouin (due aux fluctuations isentropiques de densité) et Rayleigh centrale (due aux fluctuations isobariques de densité) et Rayleigh latérale (due aux fluctuations d’orientation) ont aussi été observées en régime stimulé. Le traitement théorique ne fait pas appel à la notion de susceptibilité: la matière est traitée classiquement et macroscopiquement. Par exemple, pour les diffusions Brillouin et Rayleigh centrale, ce sont les équations de l’hydrodynamique linéarisées qui permettent de calculer la réponse du milieu. Ces phénomènes changent radicalement si le milieu est absorbant pour les ondes lumineuses.

L’optique non linéaire ne s’arrête pas au troisième ordre. Il est, par exemple, un cas qui peut être traité exactement. C’est celui d’un système à deux niveaux (a et b ) en interaction avec une onde résonnante. Tout système à deux niveaux est équivalent à un spin 1/2, ce qui a donné naissance au formalisme du spin fictif. On a observé des phénomènes comme l’écho, la nutation optique, le passage adiabatique rapide et un effet propre à l’optique: la transparence auto-induite. La saturation incohérente d’un système à deux niveaux est aussi un effet d’optique non linéaire.

Encyclopédie Universelle. 2012.